Equation d’un cercle [Vidéo](Première)
Voici 2 vidéos qui vont te permettre de trouver une équation de cercle connaissant son centre et son rayon ou connaissant son diamètre.
Tu apprendras aussi à reconnaître une équation de cercle et à trouver son centre et son rayon.
Voici la partie 1 sur les équations de cercles :
Voici la partie 2 sur les équations de cercles :
Je t’invite à télécharger la feuille d’exercices pour t’entraîner à reconnaître ou à déterminer une équation de cercle à partir de son centre et de son rayon ou à partir de son diamètre.
Pour vérifier tes résultats, voici le corrigé des exercices sur les équations de cercles.
Cette vidéo t’a-t-elle été utile ? Saurais-tu maintenant déterminer une équation de cercle ?
Laisse ta réponse dans les commentaires ci-dessous !
Afficher la transcription texte des 2 vidéosFermer la transcription texte des 2 vidéos Bonjour, bienvenue sur bossetesmaths.com, ici Corinne Huet. Je vais te donner tout d’abord la formule essentielle qui va te donner une équation de cercle. Cette formule est donnée par la propriété suivante : on va se placer dans un repère orthonormé du plan OIJ et on va dire qu’un point M de coordonnées (x;y) appartient au cercle C de centre I qui a pour coordonnées (xI ;yI) et de rayon grand R si et seulement si x et y (les coordonnées de ton point M) vérifient l’équation suivante : (x-xI) au carré + (y-yI) au carré = Rayon au carré. C’est cette formule là qui est une équation du cercle de centre I et de rayon R. Alors tu dois certainement te demander d’ou elle vient cette formule. Hé bien regarde, la démonstration est simple. Si tu prends un point M de coordonnées (x;y) qui appartient au cercle, est-ce que tu es d’accord que ce point appartient au cercle si et seulement si la longueur IM est égale en fait au rayon ? Alors comme ce sont des longueurs, on peut les mettre au carré donc c’est équivalent à dire que IM au carré est égal au rayon au carré. Mais je ne sais pas si tu t’en rappelles, dans tes cours de seconde tu as une formule pour IM au carré qui est en fait la formule suivante : (xM – xI) au carré + (yM – yI) au carré, c’est la formule de la distance et donc c’est égal à R au carré. Alors ici xM et yM en fait on les a notés x et y et donc tu te retrouves bien avec (x – xI) au carré + (y-yI) au carré = rayon au carré. Donc retiens bien le fait qu’un point M de coordonnées (x;y) appartient au cercle de centre I et de rayon R si et seulement si ses coordonnées x et y vérifient cette équation qui est une équation de cercle. Alors je te propose maintenant de traiter des exemples pour bien appréhender cette formule d’équation de cercle. Alors je reprend mon stylo pour traiter la question a; Alors si j’appelle C le cercle recherché, est-ce que tu te rappelles que son équation est de la forme (x – xI) au carré + ( y – yI) au carré = R au carré, ce qui va nous donner en remplaçant (x – xI qui vaut 4) au carré + ( y – yI qui vaut (-1)) = R qui vaut 3 au carré. Au final cela va me donner ( x – 4) au carré + ( y + 1) au carré = 9. C’est l’équation que l’on avait obtenu dans Géogébra. On peut passer à la question suivante. Question b : ce cercle passe t’il par le point A de coordonnées (1;-1) ? Allons se faire une idée sur Géogébra avant d’y répondre. Alors dans la ligne de saisie en bas, j’entre les coordonnées du point A et je vois ici apparaître mon point A sur le cercle. Démontrons réellement qu’il appartient à ce cercle ! Question b, pour démontrer que le point A de coordonnées (1;-1) appartient bien à cercle, hé bien dans l’équation je vais remplacer x et y par xA et yA donc je vais avoir à calculer (xA – 4) au carré + (yA – 1) au carré et je vais voir si l’équation est vérifiée c’est-à-dire si le résultat est égal à 9. Allons y, xA je le remplace par 1 – 4 au carré + ( ya que je remplace par -1 + 1) au carré. Je calcule les parenthèses, 1 – 4 ça nous donne (-3) au carré + (-1 + 1) ça nous fait 0 au carré = 9 donc l’équation est vérifiée par les coordonnées du point A, je peux donc conclure sans problèmes que le point A appartient au cercle C. Pour la question c, c’est le même principe : est-ce que ce cercle passe par le point B de coordonnées (6;-3) ? Hé bien je vais remplacer dans l’équation x et y par les coordonnées du point B et vérifier que le résultat est bien égal à 9. Allons y, (xB – 4) au carré + (yB + 1) au carré, ça nous donne (6 – 4) au carré + ((-3) + 1)) au carré, on calcule les parenthèses 2 au carré + -2 au carré, cela nous donne 4 + 4 = 8 donc ça n’est pas égal à 9. Le résultat est différent de 9, on peut donc dire que le point B n’appartient pas au cercle C. Regardons rapidement sur Géogébra, je saisie en bas les coordonnées de B (6;-3) et tu vois bien que le point B n’appartient pas au cercle. On passe à l’exemple 2 : Il s’agit de déterminer l’ensemble que j’ai noté E de tous les point M de coordonnées (x;y) qui vérifient (x + 3) au carré + (y – 2) au carré = 5. Et il faut préciser les éléments caractéristiques de cet ensemble E. Alors l’ensemble E est donné par l’équation suivante : (x + 3) au carré + (y – 2) au carré = 5. Tu dois prendre l’habitude de détecter les équations de cercle. Je te rappelle qu’une équation de cercle est de la forme : (x – xI) au carré + (y – yI) au carré = Rayon au carré, donc l’équation que tu as là pour l’ensemble E hé bien essaie de la mettre sous cette forme là. Cela va nous donner (x – (-3)) au carré + (y – 2) au carré (il ne bouge pas car on a bien un signe moins) = Rayon au carré, donc ici pour que ça fasse 5, je n’ai pas le choix je vais mettre racine de 5. Donc qu’est-ce que tu repères dans cette équation ? Hé bien ici tu vois bien que tu vas avoir xi, ici tu as avoir yi et ici grand R le rayon. Donc moralité, l’ensemble E est le cercle de centre I qui a pour coordonnées (-3;2) et de rayon R qui vaut racine de 5. Alors on peut maintenant passer au 3ème exemple, il s’agit de déterminer l’ensemble que j’ai noté grand F des points M de coordonnées (x;y) qui vérifient l’équation x au carré + y au carré – 4x + 5y – 10 = 0 et de préciser les éléments caractéristiques de cet ensemble F. Alors on y est presque : ici on a bien notre (x – xI) au carré + (y-yI) au carré = R au carré alors ici j’ai 81/4, est-ce que tu es d’accord que 81/4 c’est (9/2) au carré ? Donc on a bien une équation de cercle et on peut donc dire que l’ensemble F recherché est le cercle avec pour éléments caractéristiques de centre I de coordonnées (2;(-5/2)) et de rayon R = 9/2. Alors ce que je viens de te montrer, c’est une méthode classique pour pouvoir retrouver une équation de cercle ou l’on peut voir les coordonnées du centre et du rayon à partir d’une équation développée comme ceci donc il va falloir que tu t’entraînes pour pouvoir y arriver sans hésitation. Alors sur Géogébra, si je saisie en bas l’équation de l’ensemble F, tu vois bien que l’on obtient bien un cercle donc ce type d’équation est bien une équation de cercle et tu vois ici l’équation sous forme visible c’est-à-dire les coordonnées du centre qui sont ici (2;-2,5) et ici le rayon au carré donc si tu fais la racine du carré, tu retrouves bien nos 9/2 que l’on a trouvé par calcul. Pour vérifier si tu as bien compris on va terminer par une 4ème et dernier exemple dans lequel tu dois dire si l’équation x au carré + y au carré – 6x + 11 = 0 est une équation de cercle. Si oui, évidemment préciser son centre et son rayon. Hé bien c’est la fin de cette 1ère partie de vidéo sur la notion d’équation de cercle. J’espère qu’elle t’aura permis de pouvoir déterminer une équation de cercle voire même de reconnaître une équation de cercle. Alors je t’invite, pour poursuivre cette étude, à visionner la 2ème partie de cette vidéo dans laquelle tu apprendras à déterminer une équation de cercle grâce à son diamètre et ça utilisera la notion de produit scalaire. Alors je te dis à tout de suite sur bossetesmaths.com pour une 2ème partie de vidéo, salut ! EQUATION D’UN CERCLE (PARTIE 2) Bonjour et bienvenue sur bossetesmaths.com, ici Corinne Huet. Je te retrouve dans une 2ème partie de vidéo sur la notion d’équation de cercle. Dans cette vidéo, je vais t’apprendre à déterminer une équation de cercle à partir de son diamètre et ça va faire intervenir la notion de produit scalaire. A tout de suite ! Alors on entre dans le vif du sujet : comment obtenir une équation du cercle de diamètre AB lorsqu’on connait les deux points A et B ? Voici la propriété qui permet d’y répondre : Le cercle C de diamètre AB est l’ensemble des points M tels que le produit scalaire des vecteurs AM et BM est nul, est égal à 0. Pourquoi ça ? Hé bien un point M sera sur le cercle si et seulement si le triangle AMB est rectangle en M. Est-ce que tu es d’accord qu’un point sera sur le cercle si et seulement si j’ai un angle droit ici dans le triangle AMB ? C’est une propriété que l’on voit au collège. Regardons tout de suite un exercice pour comprendre cela et pour obtenir une équation de cercle grâce à un diamètre. On se place dans un repère orthonormé du plan OIj et on donne 2 points, le point A de coordonnées (-4;3) et le point B de coordonnées (2;-1) qui se situe ici. Ce que je souhaite c’est déterminer une équation du cercle de diamètre AB. Donc voilà le diamètre du cercle et je veux donc une équation du cercle qui a ce diamètre. Alors comment est-ce que je vais procéder ? Hé bien je vais noter ce cercle C et je vais appliquer la propriété que l’on vient de voir c’est-à-dire qu’un point M appartient au cercle si et seulement si ici nous avons un triangle rectangle en M donc cela équivaut à dire que le vecteur AM scalaire le vecteur BM = 0, les vecteurs sont orthogonaux. Hé bien cette 2ème partie de vidéo plutôt courte sur les équations de cercle est à présent terminée. J’espère qu’avec la 1ère partie les équations de cercle n’auront plus de secrets pour toi, que tu sauras les déterminer sans problèmes et les reconnaître aussi sans problèmes. Pour t’entrainer je t’invite à télécharger la feuille d’exercices juste en bas de ces vidéos et de te corriger grâce à la feuille corrigée que tu peux également télécharger librement. Voilà je te remercie d’avoir suivi ces vidéos sur bossetesmaths.com et je te dis à très bientôt, salut !
EQUATION D’UN CERCLE (PARTIE 1)
Alors dans cette 1ère partie de vidéo, je vais t’apprendre à déterminer une équation d’un cercle et à reconnaître une équation d’un cercle. Et nous verrons dans une 2ème partie de vidéo, comment déterminer une équation d’un cercle à partir d’un diamètre. Je te dis à tout de suite !
Dans l’exemple 1 petit a, on te demande de donner une équation du cercle de centre I de coordonnées (4;-1) et de rayon 3. On va regarder tout de suite sur un logiciel de géométrie ce qu’il se passe.
Voici l’interface du logiciel Géogebra, tu as en bas une ligne de saisie dans laquelle je vais entrer les coordonnées (4;-1) du centre de mon cercle. Alors il l’a appelé A donc je vais le renommer moi et l’appeler comme dans l’exercice 1 donc voilà mon point I et je vais donc tracer le cercle de centre I et de rayon 3 comme proposé dans l’exercice. Le voici tracé et tu vois apparaître ici en haut à gauche une équation de ce cercle à savoir (x – 4) au carré + (y+1) au carré = 9, on va tout de suite démontrer cette équation par calculs.
Alors si je retourne dans Géogébra et que je saisis l’équation donnée dans l’énoncé, tu vois bien que l’ensemble E recherché est un cercle. Alors on avait trouvé comme centre le point de coordonnées (-3;2), voilà donc tu vois bien ici le point A placé et le centre du cercle ses coordonnées sont (-3;2) et si je trace le cercle de centre A et de rayon racine de 5 (alors la racine dans Géogébra ça s’écrit sqrt) et que je fais ok, hé bien le cercle tracé de centre A et de rayon racine de 5, tu vois qu’il s’est superposé au tout premier cercle donc l’ensemble E recherché est bien le cercle de centre A de coordonnées (-3;2) et de rayon racine de 5.
Alors notre ensemble F a pour équation x au carré + y au carré – 4x + 5y – 10 = 0. Alors vu comme ça, on ne voit pas qu’il s’agit d’un cercle. En fait je vais te donner une petite astuce : quand tu vois une équation dans laquelle il y a des x carré, des x, des y carré, des y et des constantes, hé bien en général il s’agira d’un cercle. Alors on va le démonter. Tu te souviens qu’un cercle est donné par une équation du type (x – xI) au carré + (y – yI) au carré = R au carré. Hé bien je vais essayer de transformer cette équation pour avoir une équation de ce type là. Regarde comment est-ce qu’on fait ça ! Tout d’abord, tu vas rassembler les x donc on va avoir x au carré – 4x, puis les y donc + y carré + 5y – 10 (qu’on laisse ici) = 0. Alors ensuite au niveau des x, on va reconnaître le début d’une identité remarquable, ici elle sera du type x – quelque chose au carré. Alors qu’est-ce que je vais mettre ici pour que ça me donne (x au carré – 4x) ? Qu’est-ce que tu penses si je mets un 2 ici ? Qu’est-ce que ça va nous donner (x – 2) au carré quand on va le développer ? Donc ça va nous donner x au carré – 4x + 4 donc tu vois que j’ai bien mon x au carré – 4x sauf que ça fait plus 4 en plus donc il va falloir que je fasse – 4 pour pouvoir enlever ce terme en trop. Et tu vas procéder exactement de la même manière avec les y. Donc tu vois ici les y, on va essayer de détecter le début d’une identité remarquable qui sera du type (y + quelque chose) au carré. Alors qu’est-ce que je vais mettre ici pour que, quand je vais développer ce carré, ça me donne (y au carré + 5y). Donc le y au carré, je l’aurai et ici je vais rajouter 5/2. Alors pourquoi ? Qu’est-ce que ça va donner quand je vais développer (y + 5/2) au carré ? Tu vois bien là qu’on a le début de l’identité remarquable, on a bien (y au carré + 5y) sauf que ce plus 25/4 il est en trop donc il va falloir l’enlever en faisant – 25/4. Voilà et on recopie le reste de notre équation – 10 = 0. Et ensuite qu’est-ce qu’on va faire ? Hé bien on va garder les carrés (x – 2) au carré + (y + 5/2) au carré et on va mettre toutes les constantes dans le membre de droite donc ça nous fait 4 + 25/4 + 10. Voilà enfin on va calculer les constantes donc les carrés on les laisse : (x – 2) au carré + (y + 5/2) au carré = ici on va tout mettre sur 4 et au final on va obtenir 81/4.
Alors je réécris l’équation x au carré + y au carré – 6x + 11 = 0. On aimerait obtenir une équation de cercle, je te rappelle encore une fois la formule (x-xI) au carré + (y-yI) au carré = R au carré. Donc on part de cette forme développée et on essaie de la mettre sous cette forme là. Donc comme je t’ai expliqué précédemment, on regroupe les x (x au carré – 6x), on regroupe les y alors là on a que y au carré + 11 = 0. Ensuite au niveau des x on essaie de repérer une identité remarquable (x – quelque chose) au carré. Ici pour que ç fasse – 6x je vais avoir un 3 : en effet quand tu vas développer (x – 3) au carré, cela va te donner x au carré – 6x + 9. Donc tu reconnais bien x au carré – 6x et tu ne veux pas du +9 donc tu vas faire -9 + même chose pour les y, on repère une identité remarquable donc (y + ici il est tout seul donc ça sera 0) au carré + 11 = 0. On a donc nos carrés (x – 3) au carré + (y + 0) au carré = 9 – 11 = -2. Et là que se passe t’il ? Ici tu devrais obtenir un rayon au carré c’est-à-dire un carré, un nombre positif donc moralité on a bien le début d’une équation de cercle mais on n’a pas la fin, on devrait avoir un nombre positif ici donc cette équation donnée au début n’est pas une équation d’un cercle. Alors pour te convaincre que l’équation donnée n’était pas une équation d’un cercle, je suis revenu dans Géogébra et je vais saisir en bas l’équation donnée, je fais entrer et il ne se passe rien sur mon écran. On ne m’a pas tracer de cercle, on ne m’a rien tracé tout simplement puisque cette équation est impossible.
Donc si j’ai un angle droit ici en M ça veut dire que le vecteur MA et le vecteur MB sont orthogonaux. Es-tu d’accord ? Ou encore que le vecteur AM et le vecteur BM sont orthogonaux, c’est la même chose. Donc ça signifie que leurs produit scalaire est bien égal à 0. Voilà donc si tu connais le diamètre du cercle, tu pourras déterminer l’équation (en tout cas une équation) du cercle grâce à cette formule : vecteur AM scalaire vecteur BM = 0.
Alors si on note M de coordonnées (x;y), à ce moment là on peut calculer les coordonnées du vecteur AM avec la formule habituelle (xM – xA; yM – yA) ce qui nous donne (x + 4; y – 3) donc voilà pour le vecteur AM. Je peux déterminer les coordonnées du vecteur BM de même manière (xM – xB; yM – yB) donc le vecteur BM aura pour coordonnées (x – 2; y + 1) et donc je peux calculer le produit scalaire des vecteurs AM et BM. Cela va donc nous donner, on multiplie les x (x + 4) fois (x – 2) + la multiplication des y (y – 3) fois (y + 1). On peut développer le tout alors on applique la double distributivité, cela nous donne x au carré – 2x + 4x – 8 + y au carré + y – 3y – 3, on peut mettre ça dans l’ordre suivant x au carré + y carré – 2x – 3y – 7 et donc le point M appartiendra au cercle C si et seulement si le produit scalaire est nul. Je peux donc conclure que le cercle C a pour équation ce produit scalaire c’est-à-dire x au carré + y carré – 2x – 3y – 7 = 0. Donc c’est une équation sous forme développée, tu peux appliquer la méthode vue dans la 1ère vidéo sur les équations de cercle pour pouvoir la mettre sous le forme (x – xI) au carré + (y-yI) au carré = R au carré et tu pourras avoir le centre et le rayon du cercle.
Donc voilà, c’est une méthode parmi d’autres pour pouvoir obtenir une équation de cercle à partir d’un diamètre.
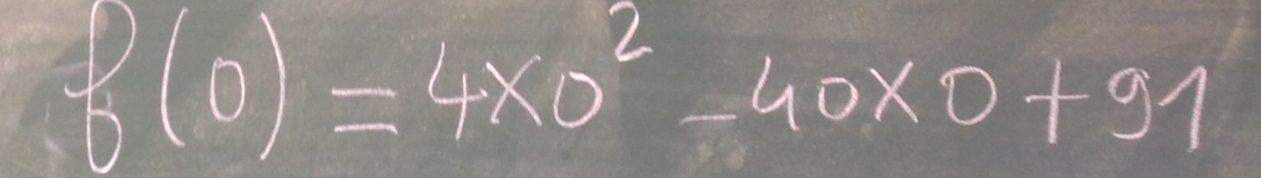

L’équation du cercle est uniquement vrai dans un repère orthonormé si je ne dis pas de bêtise.
C’est exact, tu ne dis pas de bêtise !
N’y a t-il pas une erreur dans votre développement ? AM.BM=0 (x+4) (x-2) +(y-3) (y+1) = x^2-2x+4x et vous avez mis 4 sans le x. Je ne sais pas si je me trompe :s
Effectivement, l’erreur vient de moi : je dis bien +4x et j’écris +4 en oubliant le x !!! J’ai rectifié le tir avec un correctif dans la vidéo que tu devrais voir autour de 4min40.
D’accord. Mercii beaucoup ^^
x²+y² = 25 est elle une equation de cercle comme le prouver , avec des points uniquement ?
En fait ton équation équivaut à : (x-0)²+(y-0)²=5² qui est l’équation du cercle de centre O(0;0) et de rayon 5.
Tu peux voir cette vidéo pour t’en convaincre : https://www.bossetesmaths.com/equation-dun-cercle/
Bisous, c’est encore moi Stéphane M.
Cette vidéo m’a grandement servi.
Je te trouve excellente vidéaste en math Corinne.
Bisous.
Cordialement Steph. 😉
Merci pour ton commentaire et ravie de t’avoir encore aidé !