QCM de maths : comment être plus efficace ?

Publié le par

As-tu déjà eu un QCM en contrôle ?

As-tu été déçu(e) par ta note alors que tu étais plutôt content(e) de tomber sur un QCM ?

Sais-tu qu’il y a une stratégie pour répondre à certaines questions d’un QCM de maths, et ce en ayant très peu de connaissances ?

Si ça t’intéresse, lis cet article où je vais te donner LA METHODE pour répondre aux QCM de manière optimale, avec des exemples concrets à l’appui !

Un petit rappel pour commencer : QCM sont les initiales de « Questionnaire à Choix Multiples« .

Avant d’analyser les réponses à un QCM, commençons par analyser l’énoncé du QCM.

Les 2 choses essentielles à repérer dans l’énoncé du QCM

Tu dois commencer par bien lire l’énoncé de ton QCM et repérer les 2 choses essentielles qui vont guider tes réponses :

  • Le nombre de réponses possibles : tout d’abord y a-t-il plusieurs réponses possibles ou une seule bonne réponse à chacune des questions ?
  • Le décompte des points : y a-t-il des « points négatifs » en cas de mauvaise réponse ?

Ces 2 points sont fondamentaux avant de répondre aux questions !

D’abord, s’il  y a plusieurs bonnes réponses possibles, tu peux savoir combien de réponses il faut cocher en regardant le barême du QCM.
Par exemple, si l’exercice est noté sur 10 points et qu’il comporte 5 questions, s’il y a 1 point par bonne réponse, alors tu sais qu’il faut cocher 10 réponses en tout sur les 5 questions posées, cela peut orienter tes réponses.

Sache que la tendance actuelle est de fournir aux élèves des QCM avec une seule bonne réponse possible, comme c’est le cas au Bac.

Ensuite, s’il n’est attribué aucun point négatif en cas de mauvaise réponse ou d’absence de réponse, alors fonce et réponds à toutes les questions !
En revanche, s’il y a des points négatifs, il faudra revoir cette stratégie et plutôt s’abstenir si l’on n’est pas sûr d’une réponse.

Voici un exemple d’énoncé de QCM noté sur 4 points tombé au Bac S en France en juin 2011 :

Pour chaque question, une seule des quatre réponses proposées est exacte. Le candidat indiquera sur la copie le numéro de la question et la réponse choisie. Chaque réponse exacte rapporte un point. Aucune justification n’est demandée. Aucun point n’est enlevé en l’absence de réponse ou en cas de réponse fausse.

Tu l’as compris, la stratégie ici est de répondre à chaque question (car il n’y a pas de points négatifs) avec une seule réponse possible par question.

Maintenant, venons-en à la question cruciale : quelle réponse choisir dans les choix proposés ?

Une chose est sûre : si tu as bien étudié ton cours et compris les exercices, tu sauras répondre assez bien au QCM.

Mais il y a aussi des techniques qui permettent de répondre aux questions en ayant très peu de connaissances et cela peut te faire gagner des points à tes devoirs de maths !

réponses qcm

QCM – méthode #1 : éliminer les réponses « bêtes »

Qu’est-ce que j’entends par réponse bête ? Hé bien, par exemple obtenir une probabilité supérieure à 1, ou alors une aire négative, ce genre de choses « mathématiquement bêtes » !

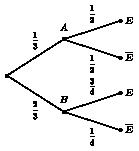
Exemple 1 : QCM Seconde

Une situation est modélisée par l’arbre pondéré suivant :

probabilité

La probabilité de l’évènement E est égale à :  a) \frac{1}{3}    b) \frac{2}{3}    c) \frac{5}{4}      d) \frac{32}{35}.

Je peux directement éliminer la réponse c) car une probabilité ne peut pas être égale à \frac{5}{4}=1,25 car une probabilité est un nombre compris entre 0 et 1 (tu le sais j’espère ? 😉 ).

Exemple 2 : QCM Terminale ES [Bac Polynésie septembre 2013]

On considère la fonction f définie sur \mathbb{R} par : f (x) = xe^{-x}.

L’intégrale \int_{0}^{1} f(x)dx est égale à : a) e-5   b) 5   c) \frac{e-2}{e}   d) 1.

Tu dois savoir 2 choses : l’intégrale d’une fonction positive est l’aire sous sa courbe donc est positive, et e\approx2,718.

Partant de là, je peux éliminer la réponse a) car f est une fonction positive sur [0;1] donc son intégrale sur [0;1] est positive, or le choix a) nous donne un résultat négatif car e-5\approx -2,28.

QCM – méthode #2 : éliminer les réponses qui donnent 2 réponses possibles

Si chaque question ne possède qu’une seule bonne réponse comme c’est souvent le cas, il faut absolument éliminer les réponses qui conduisent à une autre réponse dans la même question car on ne peut pas avoir 2 bonnes réponses (ou plus) !

Exemple 1 : QCM Seconde

Si -2\le x<3, alors : a) x^2<9   b) 4\le x^2   c)4\le x^2<9.

Tu remarqueras que si la réponse c) était vraie, alors on aurait aussi la réponse a) et la réponse b) vraies. Or il n’y a qu’une seule bonne réponse. Moralité : je peux éliminer la réponse c) !

Exemple 2 : QCM Première S

Si \vec{u} \, ^2=\vec{v} \, ^2, alors : a) \vec{u}=\vec{v}   b) \vec{u}=-\vec{v}   c) ||\vec{u}||=||\vec{v}||.

Imaginons que a) soit vraie, alors c) est vraie également. De même, si b) est vraie, alors c) est aussi vraie.

Moralité : si on répond a) ou b), alors on aura 2 bonnes réponses car c) sera automatiquement vraie. Comme il n’y a qu’une seule bonne réponse, la bonne réponse est donc forcément la réponse c) !

QCM – méthode #3 : tester chaque réponse

Parfois, il est commode de tester les réponses proposées plutôt que d’essayer de trouver la bonne réponse en utilisant les propriétés et les formules du cours. Je te montre ça sur un exemple très parlant :

Exemple : QCM Terminale ES [Bac Pondichéry avril 2012]

Soit f la fonction définie sur \mathbb{R} par : f(x)=\frac{6x-5}{3x^2-5x+7}.

On note F la primitive de f sur \mathbb{R} telle que F(1)=1.

Pour tout x \in \mathbb{R}, on a :

a) F(x)=\ln(3x^2-5x+7)
b) F(x)=\ln(3x^2-5x+7)+1-\ln(5)
c) F(x)=\frac{1}{3x^2-5x+7}+1.

La mauvaise méthode : essayer de trouver une primitive de f avec les formules des primitives. On te donne la réponse, ce n’est pas la peine d’aller chercher à trouver une primitive par toi-même !

Maintenant, comment savoir quelle réponse est la bonne ? Hé bien, il faut utiliser le fait que F(1)=1. Tu vas donc tester chacune des 3 réponses proposées en calculant F(1) et figure-toi que seule une des 3 réponses nous donne 1 comme résultat. L’as-tu trouvée ?

Il s’agit de la réponse b). En effet, la réponse a) nous donne F(1)=\ln(5)\not =1. La réponse c) nous donne F(1)=\frac{1}{5}+1\not =1. En revanche la réponse b) nous donne bien F(1)=1 !

QCM – méthode #4 : utiliser sa calculatrice

Si la question porte sur une fonction ou sur un calcul d’intégrale (en terminale), tu peux souvent utiliser la calculatrice pour y répondre.

calculatrice qcm
Image: photostock / FreeDigitalPhotos.net

Exemple 1 : QCM Seconde

Parmi les 3 fonctions suivantes, celle qui est strictement croissante sur [-1;1] est :

a) la fonction f telle que f(x)=1-x
b) la fonction g telle que g(x)=x^2
c) la fonction h telle que h(x)=x+1. 

Si tu n’as aucune idée de la réponse, prends ta calculatrice et trace la courbe de ces 3 fonctions.
Puis choisis celle qui te donne « une courbe qui monte » sur l’intervalle [-1;1].

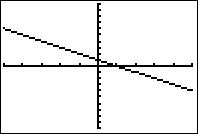
fonction f
f(x)=1-x
fonction g
g(x)=x^2
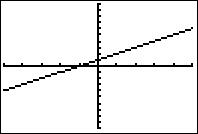
fonction h
h(x)=x+1

Les fonctions f et g ne font pas l’affaire, en revanche la fonction h a bien sa courbe qui « monte » sur [-1;1]. La bonne réponse est donc la c).

Exemple 2 : QCM Terminale ES [Bac Pondichéry avril 2013]

On pose I=\int_{0}^{1} 3e^{3x}dx. On peut affirmer que :

a) I=e^3-1
b) I=3e^3-3
c) I=19,1
d) I=1-e^3.

Ici encore, si tu ne sais pas trouver une primitive de la fonction sous l’intégrale pour pouvoir calculer cette intégrale, tu peux néanmoins calculer cette intégrale sur ta calculatrice et comparer avec les 4 résultats proposés.

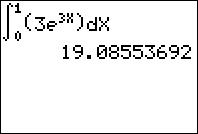
intégrale
I\approx19,0855

 

Notre intégrale I est donc environ égale à 19,0855.

Nous pouvons directement éliminer la réponse c) qui est arrondie (19,1) mais n’est pas la valeur exacte.

Pour la réponse a) : e^3-1\approx19,0855 donc on pense qu’il va s’agir de la bonne réponse.
On peut éliminer aussi la réponse d) car c’est l’opposé du résultat de la réponse a), c’est-à-dire -19,0855.

Enfin, la réponse b) nous donne : 3e^3-3\approx57,2566, on élimine donc la réponse b).

Résultat : la bonne réponse est la a).

Conclusion : comment être plus efficace face à un QCM ?

Désormais tu as quelques techniques efficaces pour être plus sûr(e) de tes réponses à un QCM de maths.

J’espère que cet article te servira à l’avenir.

As-tu trouvé cet article utile ?

As-tu d’autres techniques pour répondre à un QCM ?

Laisse ta réponse dans les commentaires juste en-dessous pour nous faire part de ton avis !