L’astuce pour retenir les formules de volume et pouvoir enfin calculer le volume d’un cylindre, le volume d’une pyramide ou le volume d’un cône !

Publié le par

Connais-tu le volume d’une pyramide ? sais-tu calculer le volume d’un cylindre ?

La plupart des élèves ont appris les formules des volumes usuels de l’espace mais les oublient 2 mois après ! Dans cet article, je vais te donner une astuce pour retenir ces formules de manière efficace et pouvoir enfin calculer sans difficulté le volume d’un solide de l’espace.

Les solides de l’espace

Voici les solides de l’espace dont tu dois absolument connaître les volumes au lycée :

  • Le parallélépipède rectangle (appelé aussi pavé droit);
  • Le prisme droit (c’est un solide qui a des rectangles comme faces latérales, toutes ses faces « de côté » sont des rectangles);
  • La pyramide;
  • Le cylindre;
  • Le cône de révolution;
  • La boule.

Voici à quoi ressemblent ces 6 solides avant de parler de leurs volumes respectifs :

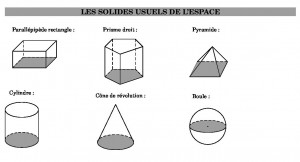
Les 6 solides usuels de l’espace

L’astuce pour retenir les volumes des solides usuels de l’espace

On va classer ces 6 solides en 3 catégories :

  • Les solides « pas pointus »;
  • Les solides « pointus »;
  • La boule.

Pour chaque catégorie, voici les formules à retenir :

Volume des solides « pas pointus »

Lorsque le solide n’est pas pointu, voici la formule de son volume :

\boxed{\mathcal{V}(\text{pas \ pointu})=\mathcal{B}\times h}

où \mathcal{B} est l’aire de la base et h est la hauteur.

Voici ce que cela va nous donner pour nos solides « pas pointus » :

  • Le parallélépipède rectangle est un solide qui n’est « pas pointu »; sa base est un rectangle de longueur L et de largeur \ell. Sa base a donc comme aire : \mathcal{B}=L\times \ell. 
    Le volume d’un parallélépipède rectangle est donc : \boxed{\mathcal{V}=L\times \ell \times h}.
Volume du parallélépipède rectangle

 

  • Le prisme droit est un solide qui n’est « pas pointu ».
    Le volume d’un prisme droit est donc : \boxed{\mathcal{V}=\mathcal{B}\times h}.
    A noter que la base d’un prisme droit peut être :
    – un triangle (alors \mathcal{B}=\frac{b\times h}{2} où b est la longueur de la base et h la hauteur du triangle);
    – un carré (alors \mathcal{B}=c^2 où c est la longueur du côté du carré);
    – un rectangle (alors \mathcal{B}=L \times \ell où L est la longueur et \ell est la largeur du rectangle);
    – etc … Bref la formule est à adapter suivant la base du prisme en question.

     

Volume du prisme droit
  • Le cylindre est un solide qui n’est « pas pointu »; sa base est un disque de rayon r.
    Sa base a donc comme aire : \mathcal{B}=\pi r^2.
    Pour calculer le volume d’un cylindre, on utilise donc la formule suivante : \boxed{\mathcal{V}=\pi r^2 h}.     

     

    • Volume du cylindre

    Volume des solides « pointus »

    Lorsque le solide est pointu, voici la formule de son volume :

    \boxed{\mathcal{V}(\text{pointu})=\frac{\mathcal{B}\times h}{3}}

    où \mathcal{B} est l’aire de la base et h est la hauteur.

    Voici ce que cela va nous donner pour nos solides « pointus » :

    • La pyramide est un solide « pointu ». Pour calculer le volume d’une pyramide, on utilise donc la formule suivante : \boxed{\mathcal{V}=\frac{\mathcal{B}\times h}{3}}.
      A noter que la base d’une pyramide peut être :
      – un triangle, la pyramide s’appelle alors un tétraèdre (alors \mathcal{B}=\frac{b\times h}{2} où b est la longueur de la base et h la hauteur du triangle);
      – un carré (alors \mathcal{B}=c^2 où c est la longueur du côté du carré);
      – un rectangle (alors \mathcal{B}=L \times \ell où L est la longueur et \ell est la largeur du rectangle);
      – etc … Bref la formule est à adapter suivant la base de la pyramide en question.
    Volume de la pyramide
    • Le cône de révolution est un solide « pointu »; sa base est un disque de rayon r.
      Sa base a donc comme aire : \mathcal{B}=\pi r^2.
      Le volume d’un cône est donc : \boxed{\mathcal{V}=\dfrac{\pi r^2 h}{3}}.
    Volume du cône de révolution 

    Volume de la boule

    Malheureusement, il va falloir apprendre cette dernière formule par coeur car la boule ne peut être classée dans l’une des deux catégories « solide pointu » ou « solide pas pointu ».

    Si la boule a pour rayon r, son volume est : \boxed{\mathcal{V}=\frac{4}{3}\pi r^3}.

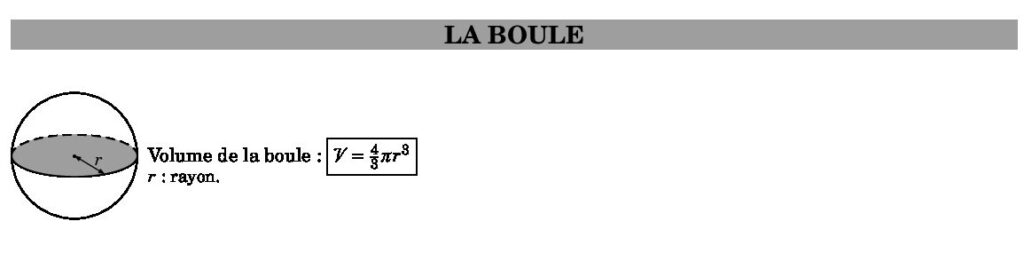
    Volume de la boule

    En résumé

    J’espère que tu as compris maintenant comment retrouver rapidement un volume usuel.

    Si ce n’est pas une boule, commence par regarder si ton solide est pointu ou non.

    Si le solide n’est pas pointu, alors son volume est : \boxed{\mathcal{V}(\text{pas \ pointu})=\mathcal{B}\times h}.

    Si le solide est pointu, alors son volume est : \boxed{\mathcal{V}(\text{pointu})=\frac{\mathcal{B}\times h}{3}}.

    Enfin, si le solide est une boule, alors son volume est : \boxed{\mathcal{V}=\frac{4}{3}\pi r^3}.

     

    Alors, penses-tu que l’astuce développée dans cet article t’aidera à retrouver les formules de volume ? 

    N’hésite pas à répondre à cette question en laissant un commentaire ci-dessous.

    Et si toi aussi tu as des astuces pour retenir des formules, partage-les en laissant un commentaire ci-dessous !

    Pour finir en s’amusant, tu peux découvrir ici comment retenir n’importe quelle formule mathématique grâce à une méthode très originale !